Network Data Science
Suman Kundu
SoNAA: Social Network Analysis and Applications (Group)
Cognitive & Social Analytics (CSA) Lab, Department of Computer Science and Engineering, IIT Jodhpur
Our Research on Networks
Fuzzy Granular Social Network
(FGSN)
Publications: Fuzzy-Rough Community, FGSN, Granular Social Network
Where
Nodes and their neighbourhood information are stored
with the help of granules defined by fuzzy sets.
What is Granule?
A granule is a clump of objects (points), in the universe of discourse, drawn together by indistinguishability, similarity, proximity, or functionality.
Why Granules?
A social network is viewed as a collection of relations
between social actors and their interactions.
These actors form closely operative groups
which are often indistinguishable in the process of problem solving.
Why Fuzzy Granules?
The basic concepts of "conceptual similarities" 'between nodes', 'cluster of nodes',
'relation between nodes and their interactions' etc. do not lend themselves to precise definition.
So, it is appropriate and natural that
a social network is represented in the framework
of Fuzzy Granulation theory
Example
FGSN: Representation
FGSN is represented by a triple $\mathcal{S} = (\mathcal{C}, \mathcal{V}, \mathcal{G})$ where,
- $\mathcal{V}$ is a finite set of nodes of the network
- $\mathcal{C}\subseteq \mathcal{V}$ is a finite set of granule centers
- $\mathcal{G}$ is the finite set of all Granules
Membership Function
A granule $g\in \mathcal{G}$ around a node ($c\in \mathcal{C}$) is defined by fuzzy membership values
In this work we use $$\begin{aligned} \mu_c(v) & = & 0 & \text{ for } d(c, v) > r \\ & & \dfrac{1}{1 + d(c, v)} & \text{ otherwise} \end{aligned}$$
- where $d(c, v)$ is the distance from $c$ to $v\in \mathcal{V}$
- $r$ is the radius of the granule
Membership Function
Further, we normalized membership values
$$\tilde{\mu_c}(v) = \dfrac{\mu_c(v)}{\sum_{i\in \mathcal{C}} \mu_i(v)} \text{ such that } \sum_{i\in \mathcal{C}} \tilde{\mu_i}(v) = 1$$Granular Degree of a Node
The degree of a node in FGSN representation, we call it Granular Degree, is defined by the cardinality of the granule centered at the node
$$\mathcal{D}(c) = |A_c| = \sum_{v\in\mathcal{V}} \tilde{\mu_c}(v)$$Granular Embeddedness of a Pair
For a FGSN, the embeddedness of any pair defines how much a granule is embedded inside the other
$$\mathcal{E}(a, b) = |A_a\cap A_b| = \sum_{v\in\mathcal{V}} \min(\tilde{\mu_a}(v), \tilde{\mu_b}(v))$$Application: Fuzzy-Rough Community Detection
Problem Statment
In the new knowledge representation of FGSN we would like to
find out densely connected groups, i.e., communities
Key Idea of Finding Communities
Identify the granules having higher density of nodes
(whose granular degree exceeds a threshold) and
Merge them if they are nearby
(merging dense regions)
$\theta$-cores
For a given $\theta$, a granule $A_p$ is said to be a $\theta$-core,
if the Granular Degree of $A_p$ is greater or equals to $\theta$, i.e., $\mathcal{D}(A_p) \geq \theta$
A community may have multiple
$\theta$-cores
The process needs to search for $\theta$-cores belonging to the same community
we call them 'Community Reachable Cores'
Three-ways of community reachability
- Directly community reachable cores
- Indirectly community reachable cores
- $r$-connected community reachable cores
Neighborhood of a Granule
Neighborhood of a granule $A_c$ is the set of all granules whose centers lie in support set of $A_c$
Directly Community Reachable
$\theta$-cores
Granules $A_p$ and $A_q$ are directly community reachable $\theta$-cores,
if $A_p$ and $A_q$ are $\theta$-cores and $A_p$ is in the neighborhood of $A_q$
Indirectly Community Reachable
$\theta$-Cores
$r$-connected community reachable
$\theta$-Cores
Community
For a given social network $\mathcal{S = (C, V, G)},
\theta,$ and $\epsilon$,
a community $\mathbb{C}$ is a non empty subset of granules $\mathcal{G}$ satisfying the following conditions:
- $\forall A_p, A_q \in{\mathbb{C}}$, $A_p$ and $A_q$ are community reachable cores
- $\forall A_p\in\mathbb{C}, \tilde{\mathcal{E}}(A_p, \bigcup_{A_q\in\mathbb{C}\setminus A_p} A_q) > 1/\epsilon$
here $\tilde{\mathcal{E}} $ is the normalized granular embeddedness defined as $\tilde{\mathcal{E}}(A_p, A_q) = \dfrac{|A_p\cap A_q|}{|A_p\cup A_q|}$
Density Co-efficient
$\theta$ controls the density of the detected communities
As $\theta$ increases, possibility of detecting more dense community increases
$\theta$ may be referred as the density co-efficient of community detection
Coupling Co-efficient
$\epsilon$ is the coupling co-efficient of the community
higher value of coupling $\rightarrow$ loosely connected groups get merged into single community
lower coupling $\rightarrow$ may result in more number of communities than actual
Fuzzy-Rough Community
Communities, thus identified, have fuzzy boundaries.
This communities can be viewed in terms of lower and upper approximations of rough set theory.
Nodes belong to the lower approximate region of a community $\rightarrow$ nodes definitely belong to.
And nodes in boundary (upper - lower) region $\rightarrow$ nodes possibly belong to.
It may be appropriate to assign fuzzy membership (0,1) to those in the boundary regions and unity (1) value to those in the lower approximate regions
Fuzzy-Rough Community: illustration
Normalized Fuzzy Mutual Information (NFMI)
$$NFMI(\mathbb{C}^X:\mathbb{C}^Y) = \frac{1}{2}[\dfrac{H(\mathbb{C}^X) - H(\mathbb{C}^X|\mathbb{C}^Y)}{H(\mathbb{C}^X)}$$ $$+ \dfrac{H(\mathbb{C}^Y) - H(\mathbb{C}^Y|\mathbb{C}^X)}{H(\mathbb{C}^Y)}]$$where $H(\mathbb{C}^X)$ is the information contain in fuzzy partition matrix $\mathbb{C}^X$ and $H(\mathbb{C}^X|\mathbb{C}^Y)$ is the conditional information measure which denotes the information contain in $\mathbb{C}^X$ for given fuzzy partition matrix $\mathbb{C}^Y$.
Normalized Fuzzy Mutual Information
Higher the value of NFMI larger the similarity (or relevance) between $\mathbb{C}^X$ and $\mathbb{C}^Y$
In an ideal case, i.e., when two community structures are identical NFMI will be $1$.
When two community structures are complement to each other NFMI would be $0$
NFMI can be used to measure the goodness of a community structure $\mathbb{C}^X$, given the actual one $\mathbb{C}^Y$
Result: LFR Benchmark Data
Network size = 1001, Min community size = 150, Max community size = 250. $\eta$: Avg ratio of external degree with total degree, $O_n$: Fraction of overlapping nodes
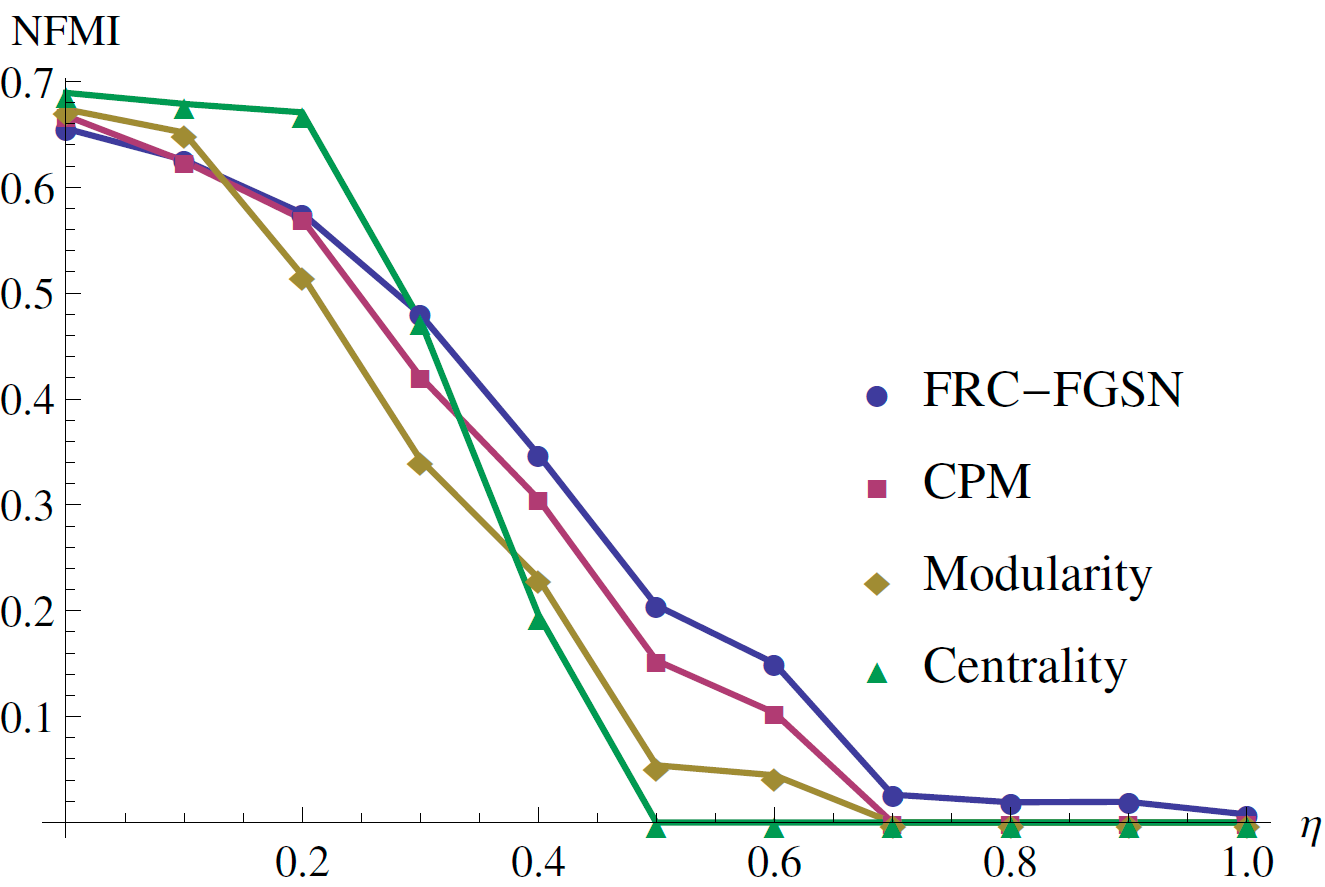
($O_n=0.15$)
NFMI for different values of $O_n$
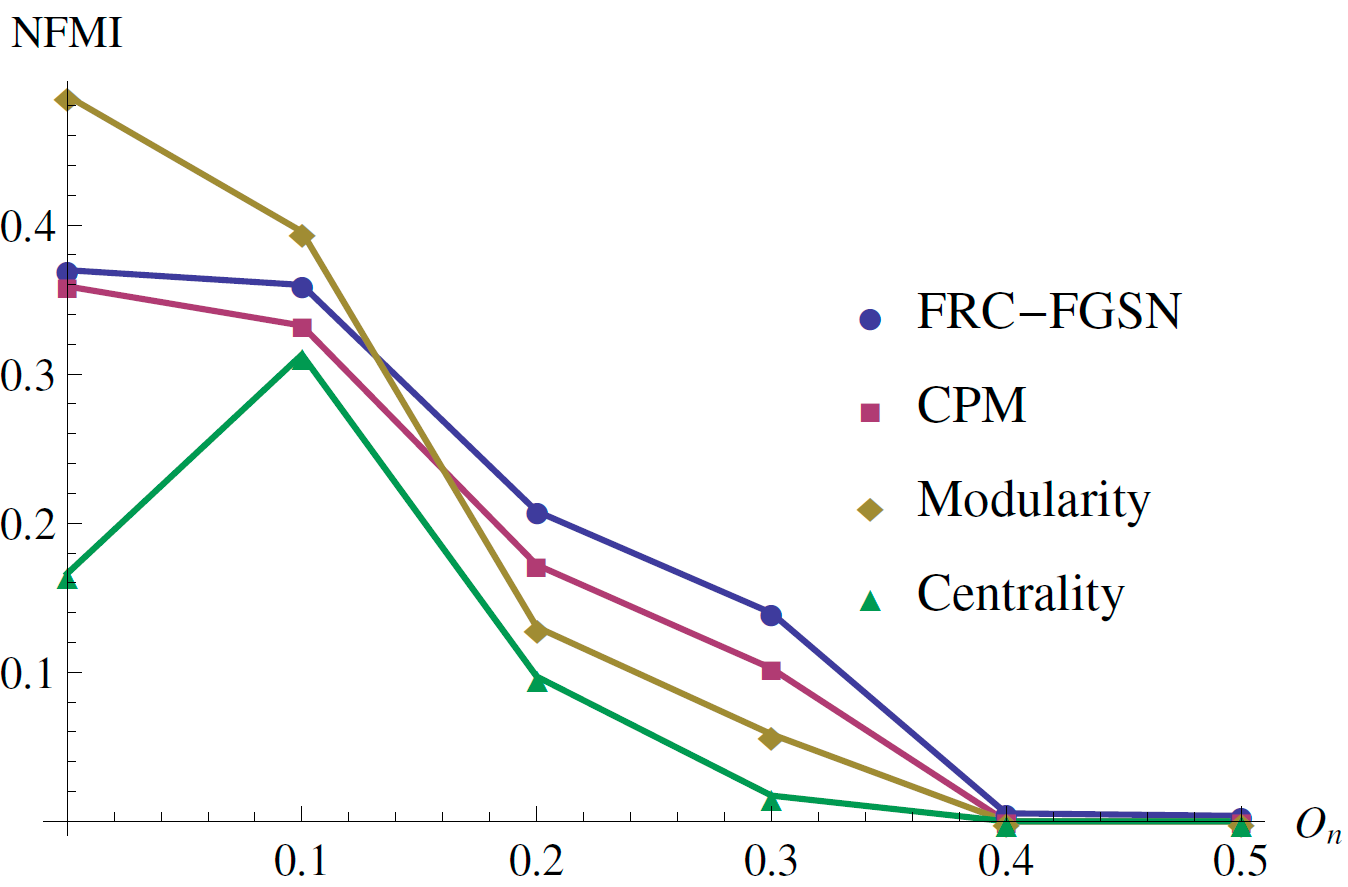
($\eta=0.4$)
Conclusion
Presented a novel knowledge representation model for social network which is based on fuzzy granulation theory.
Defined different network measures for FGSN and NFMI measure for compare two fuzzy partition matrices.
Define fuzzy-rough community and proposed an algorithm for detecting such communities using the help of FGSN